[KT] AIVLE SCHOOL 5일차
모집단과 표본
- 모집단(Population): 우리가 알고 싶은 대상 전체 영역(데이터)
- 표본(Sample): 그 대상의 일부 영역(데이터)
가설과 가설검정
- 우리는 일부분으로 전체를 추정하고자 함
- 모집단에 대한 가설을 수립
- 가설은 보통 X와 Y의 관계를 표현
- 예1: X에 따라 Y가 차이가 있다.
- 예2: X와 Y는 관계가 있다.
- 표본을 가지고 가설이 진짜 그러한 지 검증(검정)
- 가설은 보통 X와 Y의 관계를 표현
- 모집단에 대한 가설을 수립
- 어떤 시험에서 점수를 80점을 받았다면 시험을 잘 본 것일까?
- 어떤 정보를 알면 80점이 높은 지 아닌지 알 수 있을까?
- 점수 분포를 안다면 80점이 얼마나 높은지 낮은지, 흔한 결과인지 드문 결과인지 판단할 수 있음
- 비즈니스 이해단계에서 비즈니스 문제로부터 우리의 관심사(y)를 도출하고,
- y에 영향을 주는 요인(x)들을 뽑아서 초기 가설을 수립함
- 예를 들어 고객 이탈 예측(y)에 영향을 주는 요인(x)는?
- 고객의 가입 기간(x1) -> 이탈 여부(y)
- 고객의 성별(x2) -> 이탈여부(y)
- 수요량(y)에 영향을 주는 요인(x)는?
- 기온(x1) -> 수요량(y)
- 매장지역(x2) -> 수요량(y)
- 귀무가설 H0
- 영가설
- 현재의 가설
- 보수적인 입장
- 대립가설 H1
- 나의 주장
- 연구가설
- 새로운 가설
- 내가 바라는 바
- H0 : 매장지역(x2)과 수요량(y)은 아무런 관련이 없다.
- H1 : 매장지역(x2)과 수요량(y)은 관련이 있다.
통계적 검정(차이에 대한 판단)
- 우리는 표본으로부터 (대립)가설을 확인하고, 모집단에서도 맞을 것이라 주장함
- 대립가설: 매장지역(x2)에 따라 수요량(y)에 차이가 있다.
- 귀무가설: 매장지역(x2)에 따라 수요량(y)에 차이가 없다.
- 얼마나 큰지 작은지 또는 흔한 결과인지 드문 결과인지 판단하려면 차이 값의 분포를 알아야 함.
- 차이가 얼마나 커야 대립가설이 맞다(차이가 있다)고 이야기할 수 있을까?
- 아래 분포는 확률밀도함수 그래프이며, 면적은 확률을 의미함
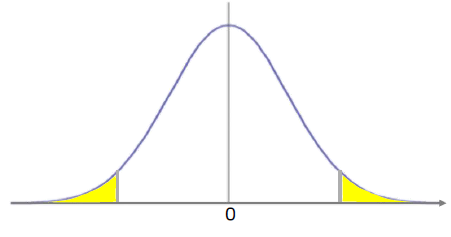
- 0에 가까울 수록 차이가 적고 흔한 결과, 0에 멀어질 수록 차이가 크고 드문 결과
- 약 5%보다 작은 영역이면
- 차이가 크다고 할 수 있음
- 대립가설이 맞다고 볼 수 있음
- 이 면적의 의미는 대립가설이 맞다고 할 때 이 판단이 틀릴 확률
검정 통계량
- 가설검정을 수행하기 위해 검정 통계량을 계산함
- t-통계량
- 𝑥²(카이제곱)-통계량
- f-통계량
- 검정 통계량은 기준 대비 차이로 계산됨
- 계산된 통계량은 각자의 분포를 가짐
- 당연히 분포를 토해서 그 값이(차이가) 큰지 작은지 판단할 수 있음
- 이를 손쉽게 판단할 수 있도록 계산해 준 것이 p-value
- p-value는 분포에서 드문 영역의 면적
유의수준, 유의확률
- 대립가설이 맞다고 받아들일 때, 틀릴 확률과 5%를 비교해 보고
- 작으면 -> 대립가설 채택(귀무가설 기각)
- 크다면 -> 귀무가설 채택
- 대립가설이 맞다고 받아들일 때 틀릴 확률 = 유의확률, p-value
- 유의수준 5%
- 5%: 피셔의 밀크티로부터 유래
- 1%: 조금 더 보수적인 기준 (예: 의학, 제조 공정 분야)
가설검정
- 오존 농도(공기 오염도)를 예측하고자 할 경우
- 우리가 세운 가설(대립가설): 온도에 따라 오존농도는 달라질 것이다.
- p-value를 구했더니 0.001이라면
- 온도 -> 오존농도, 가설이 맞다는 우리의 결정이 틀릴 확률이 0.001(0.1%)
- 기준(유의수준)으로 정한 5%보다 작으므로 우리가 세운 가설이 (모집단에서) 맞을 것이라고 판단할 수 있음
- 이러한 절차를 가설검정이라고 함
'Data Science > 데이터 분석' 카테고리의 다른 글
| 이변량 분석 (3) - 범주형 -> 범주형 (0) | 2025.04.02 |
|---|---|
| 이변량 분석 (2) - 범주형 -> 수치형 (0) | 2025.04.02 |
| 이변량 분석 (1) - 수치형 -> 수치형 (0) | 2025.04.01 |
| 단변량 분석 (2) - 범주형 (0) | 2025.04.01 |
| 단변량 분석 (1) - 수치형 (0) | 2025.04.01 |